The iconic images of dinosaurs that we know and love, the model of our Solar System, the globe, numbers and mathematical structures, musical notations, the alphabet, the periodic table of the elements, chemical structural formulas, and weather maps are all cultural icons today. Some others, like Schrödinger’s cat and Einstein’s dice, have even entered the domain of pop culture.
So who makes these icons? Who comes up with new ways of depicting these structures?
Artist London Tsai is a mathematician who thinks like a philosopher. In his work, these three fields meet and merge. When he appeared on Eric Weinstein’s Portal recently, I was fascinated, so I asked him if he would do an interview. He came back with wonderful insights which made me think about my own work and my view on the topic of learning new things:
Visualizations are like a bridge between nature as it simply exists (with or without us) and mathematics or scientific equations on the other hand. While the beauty of equations is not easily accessible to everyone, art speaks to all of us but differently…
You create paintings, drawings, sculptures – are some mediums more suitable for some kinds of mathematical ideas than others?
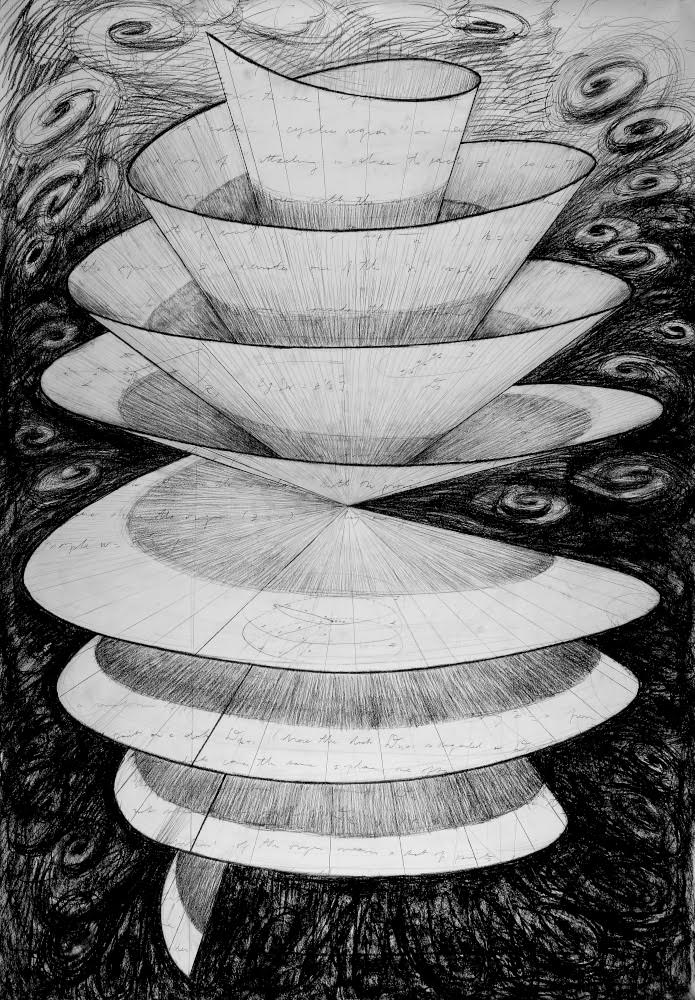
Mathematical ideas can inspire works in various mediums. An example of this in my work is the Hopf fibration, which is one of my favorite math objects; I have made numerous drawings, paintings, and sculptures of it. I think if the idea is rich enough, it lends itself to many different mediums depending on the sensitivity and taste of the artist. Of course, there are some ideas that may be too abstract for sculpture work (or at least I haven’t been imaginative enough to make sculptures from them). An example of this might be Cantor’s proof of the non-denumerability of the continuum, which I’ve only made a painting of, “Surprised Again on the Diagonal.”

Hopf Fibration N4A3488
Traditionally, linear perspective lends itself to painting and drawing as the works of the great Italian Renaissance painters attest. However, the ideas of linear perspective have found expression in contemporary 3D works, which when viewed from the right position reveal an image or writing that seems to be suspended in space. This is certainly a surprising reversal of what the Renaissance artists had originally intended!
In my case, because I have a constant flow of ideas, I often find myself choosing my medium first, which depends on where I am and what I can get my hands on. Sometimes, I have no choice and am forced to work with a certain material because of the circumstances I find myself. For example, a year ago, at the beginning of the pandemic, we were at our home in rural Upstate New York and I only had access to paper and charcoal; as a result I made several large drawings. I’ve also spent time at artist residencies in Europe; the last one in Basel took me away from my sculpture studio and all my metalworking and welding machinery. I was at a loss in the beginning, but found that I could make 3D work from cardboard that I picked up in the streets. (By the way, Switzerland has some of the highest quality cardboard I’ve ever encountered.) This harkens back to something that the sculptor Alexander Calder once said: that an artist uses whatever materials are available to them. I think the context Calder was referring to was World War II and how he managed to make work from wires and pieces of colored glass he found. In any case, I often think about that remark; it encapsulates for me what we as artists do: create expressions of our idiosyncratic selves using whatever materials and ideas that are available to us. Because of my mathematical apprenticeship, my mind is often filled with mathematical landscapes and their denizens. Meanwhile, I have a desire to make something with certain materials and processes that are available to me. So we have in me two worlds–one of mind, the other of material–that are not only simultaneously present, but are also actually sparring with one another. It is this continual superposition of these realities in my life that now and then results in artworks.
Is there a difference between beauty in the arts and beauty in mathematics?
The towering American geometer George D. Birkhoff probably didn’t think there was a difference between beauty in art and beauty in math; he wrote a book, “Aesthetic Measure,” to argue his position and presented a formula for beauty: the ratio between order and randomness. Bertrand Russell must have viewed mathematical beauty to be different from that of most art, but found this beauty in the best works of art and poetry: “Mathematics, rightly viewed, possesses not only truth, but supreme beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show.”
My own idea is that there is an overlap/intersection between beauty in art and in math, but that there are examples of each kind of beauty not belonging to the other. Of course, both kinds of beauty are somewhat subjective depending on the artist or mathematician. For example, most people would argue that the golden ratio \Phi is the best example of beauty in both art and math, but I find \Phi rather boring (probably because it’s so popular and as a result so limiting); there are so many more beautiful ideas in math that are actually experienced in the world and can be used with great effectiveness in art. The one that comes to my mind immediately is the notion of continuity versus that of discreteness.
Beauty in math is more like beauty in nature. There is an aspect of perfection that simply doesn’t exist in art; but that’s precisely what makes art human. Whenever I see a glorious sunset, I’m reminded of the fact that there is no art that I can make that can equal that kind of natural beauty. However, I do think that, at its best, my art, because it is made by me and is my interpretation of math and the world we live in, has both the beauty of math and art.

HopfFibration Photo:
Courtesy of the Artist
Can one teach maths with your art – or vice versa, can one teach art using maths?
I’m not sure that one can actually teach any subject extrinsically. To learn math, it is necessary to get deeply into it, which means struggling and wrestling with its definitions, propositions, and proofs. This requires solving difficult problems to understand profoundly how and why math is constructed in this way and not in some other less fruitful way. Unfortunately, unless you are a prodigy blessed with innate mathematical ability, you will have to endure the painful process of slowly making your way up to the heights of math. When asked by the ruler of Egypt if there was a shorter way to learn math, Euclid is said to have responded: “There is no royal road to geometry.”
On the other hand, to learn art, it is really important to train the eye by taking drawing classes and practicing drawing for years; and also working with color by painting a lot; and then sculpture requires learning how to create with various materials and the many tools needed to use them. My approach is classical and rigorous and that’s probably because of my having been the son of a well-known artist who taught me from when I was a child the painstaking processes of drawing, painting, and making sculpture.
What is possible – and this is of critical importance – is the fact that one can cultivate/inspire the appreciation of math with art; and, vice versa, one can teach the appreciation of art with math. In this way, it is possible to use one subject to bridge the other. Once the cultural divide is crossed and curiosity and interest kindled, then anything is possible: a student of art may be inspired to study math; and a student of science may begin to draw.
So, the purpose of my art is not to present/represent math to a general audience, rather it is to provide glimpses of other realities beyond the one we see around us. In this way, the works become portals that entice people to consider other different and fantastic worlds that they may even want to learn more about. And in that process they may find themselves aspiring to the noblest of what humans are capable of–probing the reality of mind and matter and finding our place in the cosmos.

London Tsai in his Studio Photo: Courtesy of the artist
Why are so many people afraid of mathematics, and how did you yourself fall in love with it?
I think one reason that people are afraid of math is that there seems to be no clear reason given for its study except that you must learn it to pass the test. So there is this stressful association people have of always being tested on math. Another reason is that math is presented in such a dry and pedantic way (there appear to be so many random rules and no room for any kind of self-expression compared to say creative writing). Grade school math is kind of like learning grammar. In high school French, we all needed to memorize the conjugation of French verbs. The purpose was not so we could be grammar experts; it was so that we could eventually read French literature and philosophy, write about it, speak to French people, watch French films, etc. I think that if math teachers could communicate clearly some of the possible reasons for studying their subject, they could motivate students to get excited about learning the material. For example, math can teach you about “infinity” and the shape of the universe; it can be used to make robots and smart phones; it can send rockets to the Moon or to Mars. And, for the pure and philosophically minded, there is simply the beauty of studying math simply for the sake of math, but these people don’t need to be told why math is worth studying: they’re the ones who love math from the start.
But I fell in love with math later than most math majors. I was the artsy kid in a competitive science high school in New York; I thought I was going to study French literature and become a poet, writer, or painter. Then I went to college and was taking French literature and calculus classes at the same time; and I found (to my great surprise!) that I was getting much more satisfaction out of math than literature. The math problems were more difficult but they made sense and there was a real structure behind it; I felt there was a quality not just of beauty but of truth. I was constructing a beautiful world inside my mind and it was filled with such eternally wondrous ideas. As Eric Weinstein said, I was hooked and math became my heroin.

To the Ends of the World
Photo: Courtesy of the Artist
When do you consider a work “complete” or “finished!, “failed”?
Some artists work on one piece at a time, but I’m not like that. I work on many at the same time; I read books the same way. I can’t remember where I got the idea, but for me a work is never finished, only abandoned. If I haven’t touched it for a couple years and I have no interest in adding any more to it, I’ll decide it’s probably done. Of course, there are works that I’ll revisit after many years later. Most of the time, an exhibition will be a determining factor: if I exhibit the work, then I usually (but not always) feel bound to not change it afterwards.
My father used to say that an artist always needs an assistant with a hammer; and their role is to knock the artist over the head when the work is finished so that he doesn’t destroy it by pushing the process too far. But because I don’t have such an assistant, I have destroyed a few works by not stopping. The one that comes back to me every now and then was my painting of Hilbert’s space filling curve: I had done the first few iterations of this curve in luminous shades blue and even exhibited it locally, but then one day I thought I could make it more interesting by adding a couple more iterations, which were not really even necessary, and the result was a complete disappointment. I had gone too far–by adding more complexity and color, my painting became much less and lost its vitality. I had killed it.
As for my studio practice, I have many different processes depending on the medium I’m working with. Curiously, people have told me that my sculptures have the same feeling as my drawings. There is a distinguishable quality that seems to be manifest in the work. I’m not sure what it is, but when I am working long and hard and “in the zone,” I feel a presence of some sort. It’s sort of an immersive automatic mode where the work appears to complete itself: I become like a vessel or conduit for its creation and accomplishment. Maybe it’s just the years of making work accompanied by the recurring thoughts that I’ve wrestled with since I first started painting with my father so many decades ago. I zoom into a section and work, then zoom out, hover and look, then zoom into another section and work some more, then zoom out again. This can go on for days, weeks, months, and sometimes years. And then one day, I find myself scrutinizing the work and not needing to change anything. And I think that maybe it’s finished, but I can’t really ever know for sure. As I mentioned above, the longer a work stays untouched and abandoned, the more likely it is to be completed.
Can you describe your studio for me?
My Brooklyn studio, which I had to give up during the pandemic, was an oasis in the city that took me several years to create. It was in an old industrial building in Sunset Park and had two levels with access to the roof where I could watch the ships and ferries coming and going in the bay of New York. Now I’ve relocated my studio to our Upstate New York property where we have a large 19th century barn on almost eleven acres of land that my parents purchased in the early 1980s. I have found that it usually takes me a couple years to get comfortable in a new space; so I’m currently in the process of getting used to this new arrangement.
I now have a painting and drawing space on an upper level; a TIG welding and metal shaping studio in the main part of the barn; and an oxy-acetylene welding studio in the lower level. The reason for being spread out is that this barn was formerly my father’s work space for his largest sculptures; I have had to carve out niches here and there to place my tools and materials to do my work. The reality of an in-house sculpture practice is that it demands a lot of space, a lot of time, and a lot of organization. At the moment, I feel a little scattered and am trying to figure out how this is going to all work. Hopefully, I will be able to settle down to make some large sculptures by summertime.
Let’s talk about your collectors, too! Is there a specific demographic of people who love and buy your art? Who are they? Where can one find your works other than the internet?
I actually don’t know who all my collectors are! But I’m pretty sure they are not for the most part “art collectors.” My feeling is that the folks that collect my work are a very diverse group, but that they share a common desire to find alternatives not just to mainstream contemporary art, but to standard dominant narratives. They are searching for answers to very deep questions that they’ve always had about reality and life; they’re looking for some sort of “portal” to transcend beyond what has been “spoon-fed” to them and to find some real meaning. It’s something I’ve also spent my life searching for and my feeling is that mathematical reality has a lot to offer in this direction.
At the moment, the Internet is the only place where my works are available. We were planning an exhibition in Paris of sculptures by my father and me when Covid-19 happened. Of course, that has been put on hold indefinitely. Unlike most professional artists, I don’t really care for the whole marketing and selling of my artwork. For me, the reward is making the artworks. You might remember the fascinating story of the great Russian mathematician Grigori Perelman who refused the Fields Medal because he felt it was unfair; he said that for him the true reward was in proving the Poincare
Conjecture. Nothing I’ve done or will ever do will come close to that, but I completely understand his position: that for people in any field, if they are truly in it for the right reasons, then the work they do is reward enough in itself.
London Tsai, Angel of History Photo: Courtesy of the artist
Eric Weinstein calls you “The Reclusive Dean of The New Escherians” Why? and how would you describe yourself? Because to me you don’t seem like a follower of Escher in a strict sense at all.
I thought Eric came up with a very creative title for our podcast. And I think I sort of forced him to come up with the novel term as I objected to being called a “mathematical artist.” I just don’t think of myself as that even if Eric sees me as a leader of this movement. Being as clever as he is, Eric thought to create the term “Escherian” and to add “New” in front of it so that I wouldn’t object directly to his calling me a follower of Escher, which you correctly surmised that I am not. But you could say that I am continuing in the spirit of Escher: namely that math is an important inspiration for my artistic practice. However, representing mathematics is not the real purpose of my work. Rather I think of my work as being humanistic and that I see math as a shining example of what humans at their best are capable of; and that one can use these ideas as ways to express what is essential about human creativity and our sense of beauty and truth.
What do you enjoy most, these days?
For the last few years, I have been really into alpine skiing. It’s something I started doing when I was a teenager that brought me tremendous joy, but I forgot about this and for various reasons I stopped skiing for a long time. And then I went again and found that it was just as wonderful as when I was young except now my body is not as strong anymore and my knees and back hurt. I think skiing has many challenges and is quite intellectual too; the key is that it is both mental and physical at the same time. There is a lot of physics going on and everything is happening so fast and so dynamically.
At the same time, there’s also a meditative/spiritual aspect to it. When you ski, you are forced to be in the moment. You have to learn to move with the flow, which means literally letting go of the past turn and saying yes to the next. It’s such an exhilarating experience: the natural setting is beautiful and the turns when done right are so elegant and majestic. It’s the closest we come to flying and I often feel like I’m riding a mathematical function, a smooth sinusoidal curve. When I am skiing and carving my way down the mountain, I forget about the mundane worries of my life and live completely in the moment. I guess it’s my heroin these days and it’s probably keeping me and my family sane in this difficult time of the pandemic.






